Liquidity Provision: Market-Making and the Avellaneda-Stoikov Model
Excerpts from my upcoming course, “A Primer on Quant Trading” (Udemy) -- part IV
Excerpts from my upcoming course, “A Primer on Quant Trading” (Udemy)
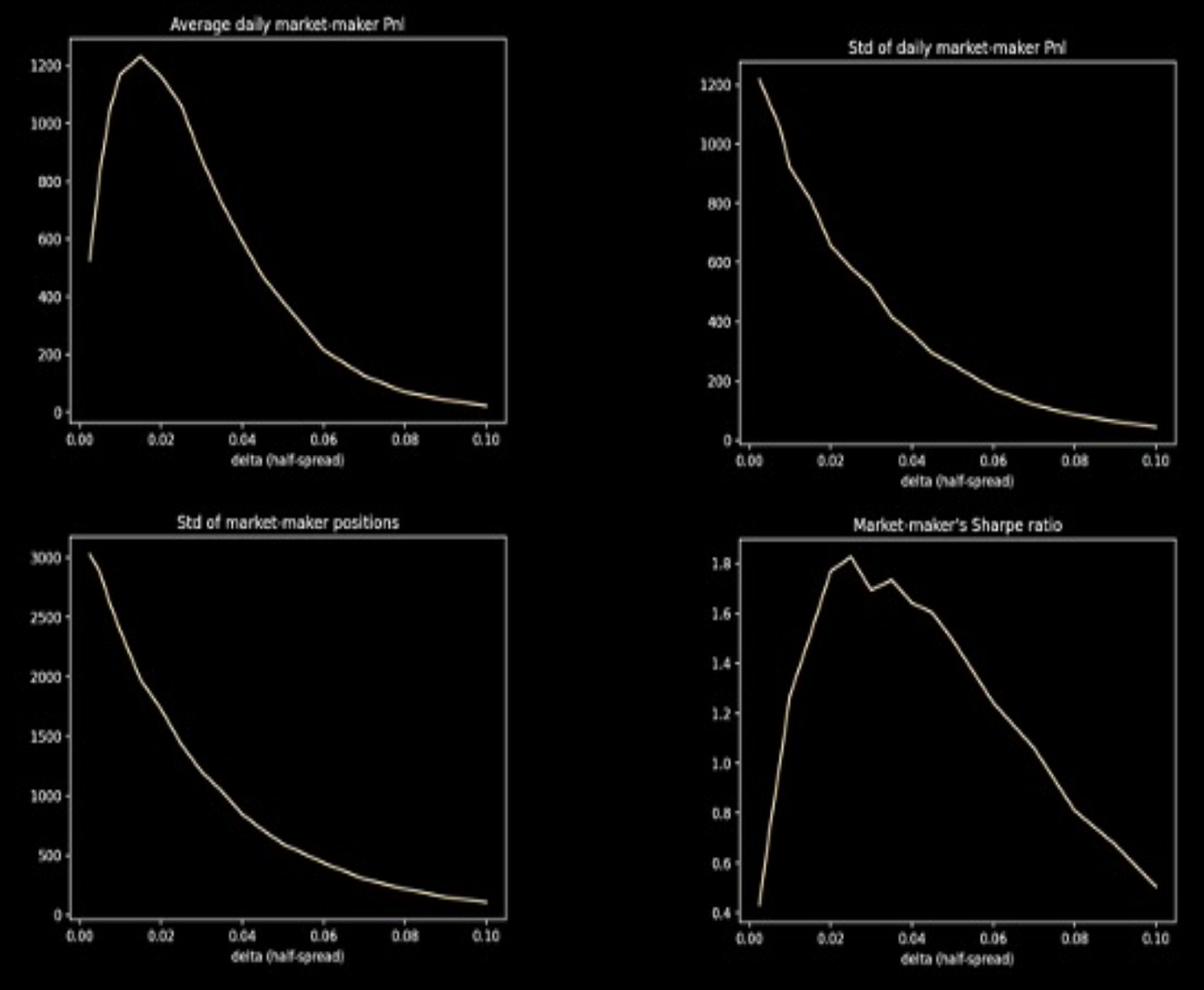
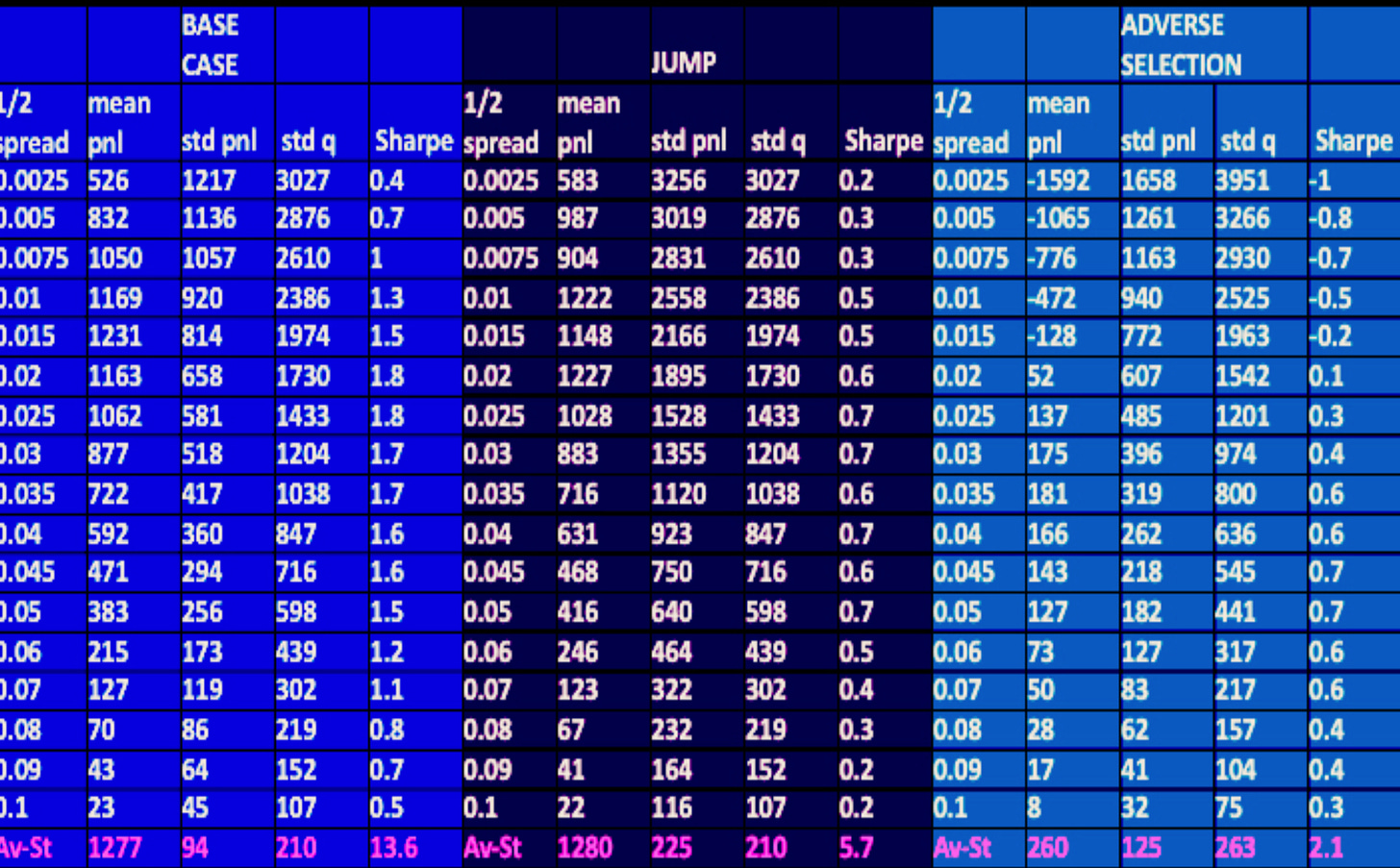
Understanding the mechanics of market-making is interesting in its own right. It is, however, also a way to understand how liquidity provision really works in practice and how it relates to market impact. In this section of my course titled “A Primer on Quant Trading”, I will start, as always, by a numerical simulation which explores how spread, volatility, and profitability are related in the simplest base case of constant-spread market-making:
Then we will learn about the limitations of this trivial case and lay down simple rules that allow the market-maker to better manage its risk. This, in turn, will lead us to the celebrated Avellaneda-Stoikov (A.-S.) model, which will be fully explained and derived from first principles, using a stochastic control approach, and its associated Hamilton-Jacobi-Bellman equation. We will solve this PDE explicitly, and provide further insight into the model.
Finally, we will examine how the A.-S. model performs relative to the naive constant-spread case, and examine its robustness to two realistic types of shocks: i) a jump in the underlying asset; and ii) toxic flow (a.k.a. adverse selection). We will show numerically, and understand conceptually, thanks to the tools we introduced, that the A.-S. model is indeed robust to mis-specifications and shocks:
If you want to learn more about the subject, stay tuned and check out my upcoming course on Udemy very shortly!
More excerpts from the course below the fold for paying subscribers.
Happy quant modeling!