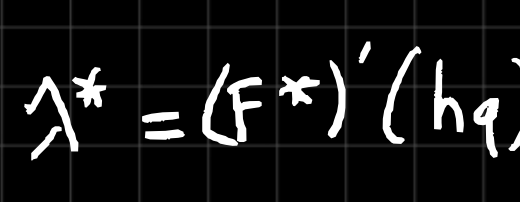On the Robustness of Constant-Speed Trading

Why the rule is optimal in a number of situations

Following up on last week’s post, let’s assume we want to add the constraint that the stock position we hold initially q_0 = Q be fully liquidated by time T: q_T = 0. Here we’ll assume no permanent market impact and a general penalization term in the value function, which will allow us to present a general method which may not be widely known (even though it is standard in the mathematical study of Hamilton-Jacobi equations). Specifically, our price, inventory, and cash processes (s_t, q_t, x_t respectively) satisfy

\((1)\ \ \ \ \ \ \begin{equation*} \left\{ \begin{split} &ds_t = \sigma dW_t\\ \\ &dq_t = - \lambda_t dt,\ \ \ \ \lambda_t>0,\ \ \ \ q_0 = Q\\ \\ &dx_t = -\left(s_t - k\lambda_t\right)dq_t, \end{split} \right. \end{equation*}\)

and the value function is defined by

\((2)\ \ \ \ \ \ u(t,x,s,q) = \sup_{\lambda_t;\ \ q_T = 0}\mathbb{E}_{t,x,s,q}\left( x_T - \int_t^Tf(\lambda_s) ds\right).\)

for a general convex function f (which was quadratic last week). The value function u is readily seen to satisfy

\((3)\ \ \ \ \ \ \begin{equation*} \left\{ \begin{split} &u_t + \frac{\sigma^2}{2}u_{ss} + \sup_\lambda\left\{ (s - k\lambda)\lambda u_x - \lambda u_q -f(\lambda) \right\} = 0\\ \\ &u(t=T,x,s,q=0) = x;\ \ u(t=T,x,s,q) = -\infty\ \ \hbox{if}\ \ q>0 \end{split} \right. \end{equation*}\)

Choosing the auxiliary function h

\((4)\ \ \ \ \ \ u(t,x,s,q) = x + qs - h(t,q)\)

leads to the following HJB equation for h:

\((5)\ \ \ \ \ \ \ \begin{equation*} \left\{ \begin{split} &h_t = \sup_\lambda\left\{ -k\lambda^2 - f(\lambda) + \lambda h_q \right\}\\ \\ &h(t=T,q) = +\infty\ \ \hbox{if}\ \ q>0;\ \ h(t=T,0) = 0 \end{split} \right. \end{equation*}\)

This easily translates into

\((6)\ \ \ \ \ \ \begin{equation*} h_t = F^*(h_q);\ \ \ F(\lambda) := k\lambda^2 + f(\lambda), \end{equation*}\)

where F* denotes the Legendre-Fenchel transform of F, and the optimal policy — optimal speed of trading λ* — is the value of λ at which the supremum in (5) is reached, namely

\((7)\ \ \ \ \ \ \lambda^* = \left(F^*\right)’(h_q)\)

Problem (6) along with the boundary condition in (5) admits an explicit solution called the Lax-Oleinik formula which, in our case, reads:

\((8)\ \ \ \ \ \ h(t,q) = (T-t) F\left( \frac{q}{T-t} \right),\)

since F**=F, f (and therefore F) being convex. From (8) we derive

\((9)\ \ \ \ \ \ h_q = F’\left(\frac{q}{T-t}\right)\)

and therefore

\((10)\ \ \ \ \ \ \lambda^* = \left(F^*\right)’\left( F’\left( \frac{q}{T-t} \right)\right) = \frac{q}{T-t}\)

since the derivatives of F and F* are inverse of each other. Now, by (1) λ* = -dq/dt, and therefore, solving (10), the optimal liquidation strategy in terms of our stock inventory q(t) is

\((11)\ \ \ \ \ \ \boxed{q(t) = Q\left(1 - \frac{t}{T}\right)}\)

which corresponds to a constant speed of selling λ* = Q/T.

From this analysis we can see why (11) is optimal in a number of situations and how the Lax-Oleinik formula can help us understand this type of problems.

Quantitatively Yours,