The Drawbacks of Drawdowns

Understanding the distribution of the Calmar ratio

One of the more useful measures of drawdowns that is used in practice, and which has the advantage of being scale-invariant, is the usual Calmar ratio:

\(\hbox{Calmar} = \frac{\hbox{Annualized average return}}{\hbox{Maximum peak-to-trough drawdown}}\)

(For instance, a Calmar of 3 means the maximum drawdown is the equivalent of (1/3) of the annual return.)

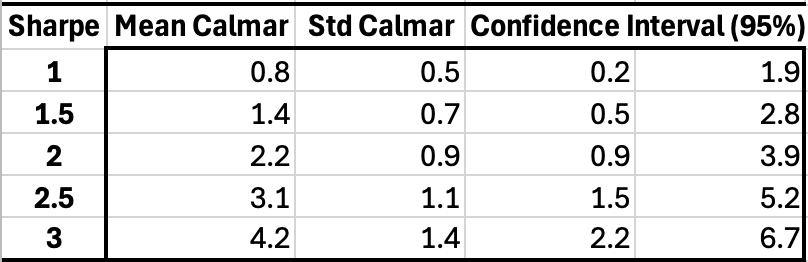
A natural question one can ask is what the average Calmar for a given Sharpe is, and what the associated confidence interval is. For that, what we’re going to do is run a Monte-Carlo simulation with 10,000 trajectories, with a given average annual return μ and volatility σ such that μ / σ = a given Sharpe. (See code below the fold.) We can summarize the results in the following table:

As an illustration, here’s the empirical distribution of the Calmar ratio for a given Sharpe = 1.5

Quantitatively Yours,

---

import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt

DisplayPlots = True

AllSR = np.array([1.0, 1.5, 2.0, 2.5, 3.0])
sigma = 0.20
T = 5
ndays = 252 * T
dt = 1 / 252
n_sims = 10000
z = np.random.normal(0,1,(ndays + 1,n_sims))
paths = np.zeros((ndays, n_sims))
results = {}
calmar_ratios = {}
for sharpe in AllSR:
    mu = sharpe * sigma # annualized
    for t in range(1,ndays):
        paths[t,:] = paths[t - 1,:] + mu * dt + sigma * np.sqrt(dt) * z[t,:]
    rolling_max = np.maximum.accumulate(paths,axis=0)
    DD = rolling_max - paths
    maxDD = np.max(DD,axis=0)
    AnnualRet = (1/T) * ( paths[-1,:] - paths[0,:] )
    valid_idx = (maxDD > 0) & (AnnualRet > 0)
    calmar_ratios[sharpe] = AnnualRet[valid_idx] / maxDD[valid_idx]

    # Store summary statistics
    results[sharpe] = {
        'Mean Calmar': np.mean(calmar_ratios[sharpe]),
        'Std Dev': np.std(calmar_ratios[sharpe]),
        'Median': np.median(calmar_ratios[sharpe]),
        '5th Percentile': np.percentile(calmar_ratios[sharpe], 5),
        '95th Percentile': np.percentile(calmar_ratios[sharpe], 95),
    }

df_results = pd.DataFrame(results).T
print(df_results)

if DisplayPlots:

    sr = 1.5
    fig, ax = plt.subplots(figsize=(12, 6))
    ax = sns.histplot(calmar_ratios[sr], bins=20, kde=False, color="yellow", stat="probability")  # <-- this is key
    plt.xlabel("value", fontsize=14) 
    plt.ylabel("frequency", fontsize=14)  # y-axis now represents frequency
    for spine in ax.spines.values():                                                                                                                               
        spine.set_color("white")  
    plt.title("Calmar for Sharpe=%1.1f" % sr, fontsize=14)
    plt.xticks(fontsize=14)
    plt.yticks(fontsize=14)

    p05 = np.percentile(calmar_ratios[sr], 5)
    p95 = np.percentile(calmar_ratios[sr], 95)
    ax.axvline(p05, color="red", linestyle="--", linewidth=2, label="5th Percentile")
    ax.axvline(p95, color="red", linestyle="--", linewidth=2, label="95th Percentile")
    plt.legend(fontsize=14)

    plt.show()